Ecole des Mines de Nantes, 4 rue Alfred-Kastler, Nantes 44307, France
Institut de Recherches en Communications et en Cybernetique de Nantes, 1 rue de la Noe, 44321 Nantes, France
(Accepted to "Mechanism and Machine Theory 46 (2011) 662–679")
Previous page | Outline | Next page
To demonstrate the efficiency of the proposed technique, let us present two examples that focus on the loaded working mode and deal with (i) the stiffness analysis of a serial kinematic chain with passive joints and (ii) the stiffness analysis of a translational parallel manipulator. Within this study, it is assumed that the external wrench is acting upon the manipulator end point and the influence of the gravity is negligible. In previous works [42], this problem was studied for the unloaded working mode and for small deflections in elastic elements, so any non-linear abnormality in the manipulator behavior (buckling, etc.) was non detected.
First, let us consider a serial kinematic chain consisting of three similar links separated by two similar rotating actuated joints. It is assumed that the chain is a part of a parallel manipulator and it is connected to the robot base via a universal passive joint, and the end-platform connection is achieved via a spherical passive joint. For each of these configurations, let us investigate three types of the virtual springs corresponding to different physical assumptions concerning the stiffness properties of the actuators/links. They cover the cases, in which the main flexibility is caused by the torsion in the actuators, by the link bending, and by the combination of elementary deformations of the links.
The geometry of the examined kinematic chain (Fig. 1) can be defined as UpRaRaSp where R, U and S denote respectively the rotational, universal and spherical joints, and the subscripts ‘p’ and ‘a’ refer to the passive and active joints respectively. Using the homogeneous matrix transformations, it can be described by the equation
where 
and 
are the elementary rotation/translation matrices around/along the z- and x-axes, 
is the homogeneous rotation matrix of the universal joint (incorporating two elementary rotations), 
is the homogeneous rotation matrix of the spherical joint (incorporating three elementary rotations), 
are the coordinates of the actuated joints, 
is the length of the links, 
is the coordinate vector of the universal passive joint located at the robot base, 
is the coordinate vector corresponding to the passive spherical joint at the end-platform, 
is the homogenous matrix-function describing elastic deformations in the links and actuators (they are represented by the virtual coordinates incorporated in the vectors 
). It is obvious that this model can be easily transformed into the form 
used in the frame of the developed technique.
To investigate particularities of this kinematic chain with respect to the external loading, let us also consider three typical postures that differ in values of the actuated coordinates:
S-configuration: the links are located along the straight line (Fig. 1a),
the actuated coordinates are
P-configuration: the chain takes a trapezoid shape (Fig. 1b),
the actuated coordinates are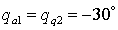
Z-configuration: the chain takes a zig-zag shape (Fig. 1c),
the actuated coordinates are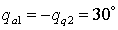
For presentation convenience, let us also assume that the coordinates 
of the universal passive joint are computed to ensure location of the end-effector on the Cartesian axis x. Besides, it is assumed that the external loading is presented by a compressing force applied at the chain end-point and it is directed along x-axis (see Fig. 1).
In order to investigate possible non-linear effects in the stiffness behavior of this chain, let us consider several cases that differ in stiffness models of the links and actuated joints:
Case of 1D-springs (Model A): the flexible elements are localized in the actuating drives while the links are considered as strictly rigid. It allows, without loss of generality, to reduce the original UpRaRaSp model down to RpRaRaRp and define a single stiffness parameter 
(similar for both actuators) that will be used as a reference value for the further analysis. Besides, it is possible to ignore the end-effector orientation and consider a single passive joint coordinate 
(at the base) and two virtual joint coordinates 
, 
(at actuators).
Case of 2D springs (Model B): the actuators do not include flexible components but the manipulator links are subject to non-negligible elastic deformations in Cartesian xy-plane (bending and compression). Correspondingly, the link flexibility is defined by a 3x3 matrix that includes elements describing deformation in x- and y- directions and rotational deformation with respect to z-axis.
Case of 3D springs (Model C): the actuators are strictly rigid but the link flexibility is described by a full-scale 3D model that incorporates all deflections along and around x-,y-,z-axes of the three-dimensional Cartesian space. Relevant stiffness matrix of the links has the dimension 6x6. The kinematics of this model corresponds to the general expression UpRaRaSp, it includes two passive joints 
incorporating in total five passive coordinates and three virtual-springs with 18 virtual coordinates totally (six for each link).
In order to simplify comparison of numerical values derived from the stiffness analysis of examined serial kinematic chains , the compliance matrices corresponding to all considered case studies were parameterized similarly. Relevant expressions are presented below.
In the case of 1D-springs (Model A), it is assumed that all flexible elements are localized in the actuating drives while the links are considered as strictly rigid. It allows to define a single stiffness coefficient 
(similar for both actuators) that is used as a reference value for other case studies.
In the case of 2D springs (Model B), it is assumed that the actuators do not include flexible components but the manipulator links are subject to elastic deformations in Cartesian xy-plane (bending and compression). Correspondingly, the link flexibility is defined by a 3x3 matrix that includes elements describing linear deformation in x- and y- directions and rotational deformation with respect to z-axis. Relevant stiffness matrix may be written as
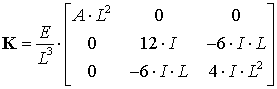
where 
is the length of the links, 
and 
are respectively its second moment and area of the cross-section , 
is the Young module. To ensure comparability with model A, the element 
(corresponding to z-rotation) of the compliant matrix 
was denoted as 
. It allows to eliminate the Young module and present the desired matrix as
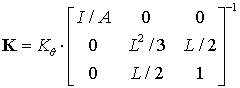
where, for the rectangular cross-section 
, the remaining parameters are expressed as 
and 
.
In the case of 3D springs (Model C), the actuators are strictly rigid but the link flexibility is described by a full-scale 3D model that incorporates all deflections along and around x-,y-,z-axes of the three-dimensional Cartesian space. Relevant stiffness matrix of the links has the dimension 6x6 and may be expressed as
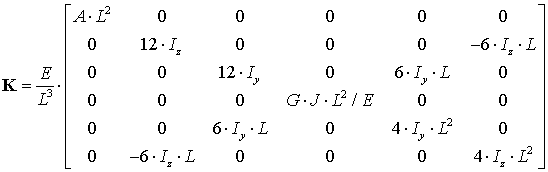
where A, 
are the area and the second moments of the link cross-section, 
is the polar moment, E and G are the Young and Coulomb modules of the material. For the rectangular cross-section 
, the required parameters may be computed as 
and 
, 
.Similar to the previous case, the parameterization is performed by defining the compliance with respect the z-axis as 
(here, it is element 
of the compliant matrix 
). This leads to expression
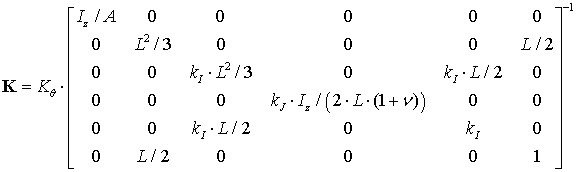
where the coefficient 
depends on cross-section shape, 
, and 
is the Poisson ratio coefficient.
In this case, the model includes minimum number of flexible elements (two 1D virtual springs in the actuated joints) and may be tackled analytically. However, in spite of its simplicity, it is potentially capable to detect the buckling phenomena at least for S-configuration, because of evident mechanical analogy to straight columns behavior under axial compression. It is also useful to evaluate other initial configurations with respect to the multiple loaded equilibriums, their stability and to compare with numerical results provided by the developed technique.
In the frame of this model, the end-effector motions are restricted to Cartesian xy-plane and the geometry is defined by equations
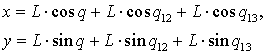
where L is the length of links, 
is the passive joint coordinate, 
are the virtual spring coordinates, 
and 
. It is obvious that this model includes exactly one redundant variable. Without loss of generality, one can assume that the redundant variable is the passive joint coordinate 
while the manipulator end-effector is initially located at the point 
, where 
is a linear displacement along x-axis. It worth mentioning that other possible deformations (along y-axis) are not considered here because, as follows from separate study, in this direction the kinematic chain is kinematically singular due to passive joint 
and, obviously, the chain does not demonstrate any non-linear phenomena in stiffness analysis that are in the focus of this paper.
Then, assuming that the initial values of the actuating coordinates (i.e. before the loading) are denoted as 
, 
, the potential energy stored in the virtual springs may be expressed as the following function of the redundant variable
where 
is the stiffness coefficient, and 
, 
are computed via the inverse kinematics. Using these equations, the desired equilibriums may be computed from the extrema of 
. In particular, stable equilibriums correspond to minima of this function, and unstable ones correspond to maxima.
To illustrate this approach, Fig. 2 presents a case study for the initial S-configuration. It allows comparing 12 different shapes of the deformated chain and selecting the best /worst cases with respect to the energy. As follows from these results, here there are two symmetrical maxima and two minima, i.e. two stable and two unstable equilibriums. Besides, the stable equilibriums correspond to P-shaped deformated postures, and the unstable ones correspond to Z-shaped postures, as it is shown in Fig. 3 More detailed analysis allows deriving analytical expressions for the force and energy for small values of d:
stable equilibrium:
;
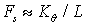
unstable equilibrium:;
Hence, the external force 
can not change the manipulator shape, similar to small compressing of straight columns that can not cause lateral deflections. Consequently, in this case the straight configuration is stable. Further, for 
, the straight configuration may be hypothetically restored but becomes unstable, so any small disturbance will cause sudden reshaping in the direction of the stable trapezoid-type posture. And finally, for 
, there may exist two types of unstable equilibriums: the trivial straight-type and a more complicated zig-zag one.
Fig 3. Evolution of the S-configuration under external loading
If the assumption concerning small values of d is released, analytical solutions for the non-trivial equilibriums may be still derived. In particular, for the stable equilibrium, one can get
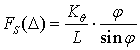
where 
, 
. For the unstable equilibrium similar equation may be written as
where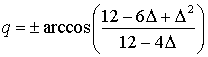 
, . 
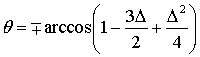
Corresponding plots are presented in Fig. 4 where there are also shown the bifurcation and analytical expressions for F corresponding to small values of 
that are derived from last two equations by parametric differentiation with respect to 
. The interpretation of this plot is similar to the axial compression of a straight column, which is a classical example in the strength of materials. It should be noted, that the developed numerical algorithm exactly produces the curve corresponding to the stable equilibrium.
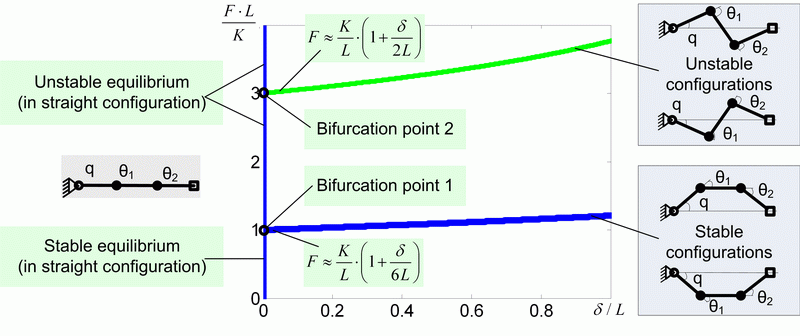
Fig.4 Model A: Force-deflection relations and bifurcations for the initial S-configuration
For other initial shapes (P-type and Z-type), the results essentially differ from the above ones (see Table 1). In particular, for small deflections, both P-and Z-configuration demonstrate rather linear behavior. Moreover, in most of the cases there exist a single stable and a single unstable equilibrium, so the kinematic chain can not suddenly change its shape due to external loading. The only exception is the case of the initial P-configuration where there are two stable and two unstable equilibriums, and here there exists a bifurcation of the stable equilibriums corresponding to the cuspidal point of the function 
where the stiffness reduces sharply. Another conclusion concerns the profile of the force-deflection plots that are highly nonlinear in all cases.
More detailed analysis shows that P-configuration demonstrates good analogy with axially compressed imperfect column where the deflection starts from the beginning of the loading and there is no sudden buckling, but the stiffness essentially reduces while the loading increases. In particular, for the examined kinematic chain the stiffness coefficient is about 
at the beginning and 
at the end of the curve 
.
However, for Z-configuration that corresponds to the unloaded zig-zag shape, the stiffness behavior demonstrates the buckling that leads to sudden transformation from a symmetrical to a non-symmetrical posture as shown in Fig. 5. Here, there exist four stable equilibriums (and two unstable ones) that differ in the values of the potential energy, so the stiffness coefficient reduces from 
at the beginning to 
at the end of the curve 
(see Fig.5).
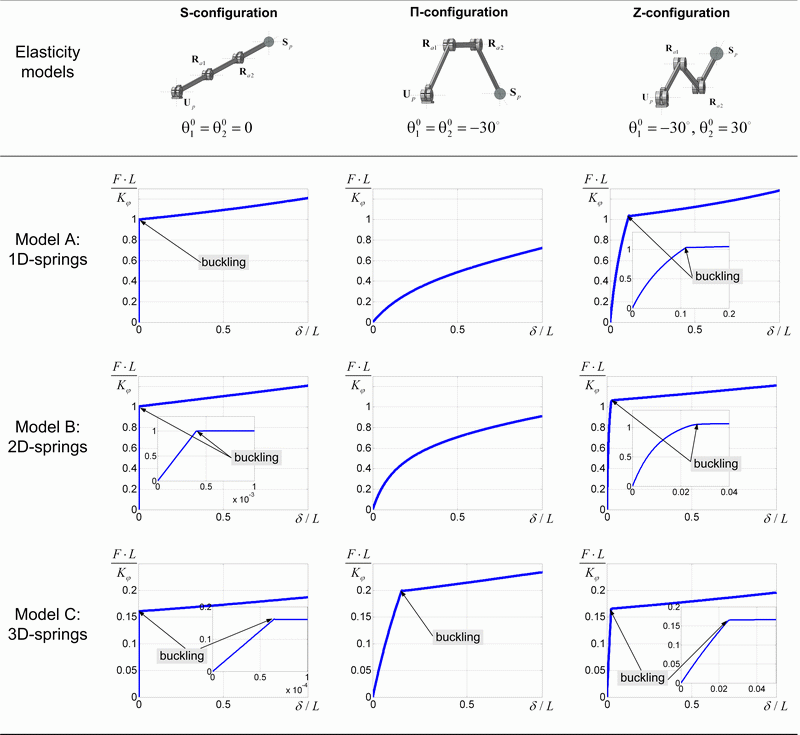
Fig.5 Force-deflection relations for different elasticity models of serial chain with passive joints
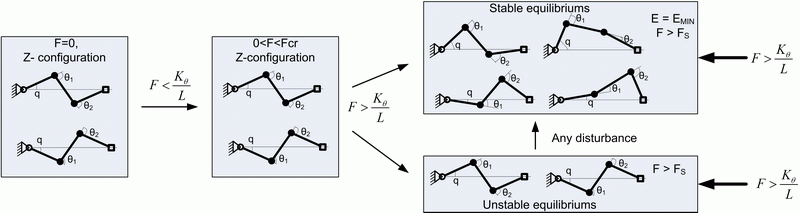
Fig.6 Evolution of the Z-configuration under external loading
Table 1 Summary of stiffness analysis for serial chain with passive joints : Model A
Configuration |
Critical
force |
Stiffness for unloaded mode |
Stiffness around the buckling |
Stiffness for large deformations (  ) |
|
 |
 |
||||
S-configuration |
 |
 |
 |
 |
 |
P-configuration |
--- |
 |
--- |
--- |
 |
Z-configuration |
 |
 |
 |
 |
 |
Hence, in the case of model A, the developed numerical technique provides results that correspond to the stable loaded equilibriums and coincide with relevant analytical solutions. Besides, it was detected more general class of manipulator postures that are dangerous with respect to buckling. They include all configurations possessing by an axial symmetry with respect to the direction of the external force (S- and Z-configurations, for instance).
In this case, the manipulator stiffness is caused by elasticity in the links while the actuating joints are assumed to be rigid. The elastic deflections (bending and compression) are still restricted by the Cartesian xy-plane but each link includes three virtual joints. Totally, the stiffness model has 11 variables, so it was studied numerically (using the developed technique). The stiffness parameters of the elements were evaluated assuming that the links are rectangular beams of the length L and the cross-section a´b, where 
and 
. For comparison purposes, corresponding stiffness matrices were scaled with respect to the bending coefficient 
, to keep similarity with model A. The stiffness analysis was performed for above defined S-, P- and Z-configurations, assuming that the external force is directed along the x-axis. Summary of the modeling results are presented in Fig.5 and Table 2 and are briefly described below.
For S-configuration, here there is still very strong analogy with the compression of the straight column. In particular, at the beginning of the loading, the links are subject the axial compression and the stiffness is very high (about 
, for the assumed link proportions). Then, after the buckling, the manipulator changes its shape to become non-symmetrical and the stiffness falls down to 
. The critical force may be also computed using the previous results, as 
.
For P-configuration, the stiffness properties are also qualitatively equivalent to the case of Model A but the stiffness coefficient is slightly lower (in the frame of the adopted parameterization); it varies from 
to 
. For Z-configuration, it was also detected the buckling that occurs if the loading approaches to the critical value 
. At this point, the stiffness falls down from 
to 
, which essentially differs from model A.
Hence, stiffness analysis of Model B demonstrates qualitative similarity but some quantitative difference compared to Model A. The latter is caused by different arrangement of the elastic elements in the virtual joints that corresponds to other physical assumptions.
Table 2 Summary of stiffness analysis for serial chain with passive joints : Model B
Configuration |
Critical
force |
Stiffness for unloaded mode |
Stiffness around the buckling |
Stiffness for large deformations ( ) |
|
|
|
||||
S-configuration |
|
 |
 |
 |
|
P-configuration |
--- |
 |
--- |
--- |
|
Z-configuration |
|
 |
 |
 |
|
Finally, for model C, the link elasticity is described in 3D space and corresponding stiffness matrices have dimension 6x6 (the actuating joints are assumed perfect and rigid, similar to model B). It is also assumed that the links are rectangular beams of the length L with the cross-section a´b, where 
, 
and the smaller value 
corresponds to z-direction, which was not studied above. To ensure comparability of all examined cases, the link stiffness matrices were parameterized with respect to the bending coefficient of the z-axis
. In total, the stiffness model includes 23 variables (five for passive joints and 18 for the virtual springs of three links) and it was studied numerically. The stiffness analysis was performed for the same initial configurations (S-, P- and Z-type) and for the same direction of the external force as for the models A and B.
For S-configuration, the results are qualitatively similar to ones obtained for model B. Besides, numerical value of the stiffness for the non-loaded case is the same, 
. However, here the buckling occurs for essentially lower critical force, 
, that corresponds to sudden lateral deflection in z-direction (For comparison, according to the Euler formula, the local buckling of the links occurs for compressing force of 0.40 Kq/L, which is 2.5 times higher than the loading that provokes the geometric buckling of the examined mechanism.). Then, after the buckling, the stiffness falls down to 
. It is worth mentioning that the axial deflection corresponding to the critical force is very low, it is equal to 
.
In contrast, for P-configuration, it was detected buckling which does not exist in models A and B. In particular, if the external force exceeds the critical value 
the stiffness suddenly reduces from 
to 
(for comparison, the stiffness coefficient for unloaded mode is 
). Physically it is also explained by sudden deflection in z-direction that it was beyond capabilities of previous models. It is worth also mentioning that, in this case study, the stiffness of manipulator links in z-direction is essentially lower than in y-direction. Another interpretation of this buckling phenomenon may be presented as sudden loss of symmetry with respect to xy-plane.
For Z-configuration, the results remain qualitatively the same as above, but corresponding numerical values are changed. Thus, manipulator stiffness for the unloaded mode is 
, then it gradually reduces to 
and, after buckling, falls down to 
. Corresponding value of the critical force is 
and it also corresponds to the z- deflection.
Summarized results concerning all models A, B, C are presented in Fig.5 and Tables 1-3. As it follows from them, a full-scale 3D stiffness analysis yields essentially lower values of critical force compared to models A and B. Besides, for model C, all examined postures demonstrated buckling related to sudden deflections in the z- direction. This presents another source of potential structural instability of kinematic chains that posses the symmetry with respect to a plane.
Table 3 Summary of stiffness analysis for serial chain with passive joints : Model C
Configuration |
Critical
force |
Stiffness for unloaded mode |
Stiffness around the buckling |
Stiffness for large deformations ( ) |
|
|
|
||||
S-configuration |
|
 |
 |
 |
|
P-configuration |
|
 |
 |
 |
|
Z-configuration |
|
 |
 |
 |
|
and geometric postures for different values of 
)
