Enhanced stiffness modeling of manipulators with passive joints

Ecole des Mines de Nantes, 4 rue Alfred-Kastler, Nantes 44307, France
Institut de Recherches en Communications et en Cybernetique de Nantes, 1 rue de la Noe, 44321 Nantes, France

(Accepted to "Mechanism and Machine Theory 46 (2011) 662–679")

Previous page  |  Outline  |  Next page

A: Algorithms for stiffness modeling

A.1  Pseudocode for computing of equilibrium configuration for given end-effector location

Algorithm A1   
Computing of equilibrium configuration  and external loading for given end-effector location  (for serial chain)

INPUT:		end-effector location
OUTPUT:		equilibrium configuration
		external loading
		stiffness matrix
PARAMETERS:		maximum number of iterations
		compliance matrix of elements
		internal preloading
		calculation accuracy
		weighting coefficients
INTERNAL FUNCTIONS:		geometry function

   Begin

(1) initialization

(a) set initial configuration

;     ;      from inverse kinematic for unloaded mode

(b) disturb configuration with random noise

,

(c) set loop variables

(2) main loop

       while  do

(a) compute Jacobians for configuration

(b) compute new configuration  and loading

(c) redefine loop variables 

(d) compute residuals

(e) verify termination condition

(I) if   then     

(II) if             then     

       end (2)

(3) check stability of equilibrium configuration

(a) if

then

(I) compute Hessians of function

(II) compute SVD for Jacobians

(III) extract  corresponding to zero elements of

(IV) verify stability condition

if        

then     message(“Static equilibrium is stable”)    

else     message(“Static equilibrium is unstable”)

(b) if               then     message(“Solution was not found”)

(4) Compute stiffness matrix

if      then

   End

A.2  Pseudocode for computing of equilibrium configuration for given external loading

Algorithm A2
Computing of equilibrium configuration for given external loading   (for parallel manipulator)

INPUT:		external loading
		end-effector location  for unloaded mode
OUTPUT:		end-effector location
		stiffness matrix
PARAMETERS:		number of kinematic chains
		number of passive joints  in  chain
		number of virtual joints  in  chain
		stiffness matrix of elements  for  chain
		internal preloading  in  chain
		weighting coefficient
		calculation accuracy
		maximum number of iterations
INTERNAL VARIABLES:		equilibrium configuration  for  chain
		loading  in  chain
		stiffness matrix  for  chain
INTERNAL FUNCTIONS:		geometry function  for  chain
		potential function  for  chain

   Begin

(1) initialization

(a) set initial configuration for all chains

;    from inverse kinematic for unloaded mode, 

(b) set initial end-effector location

(c) set external loading for chains

, 

(b) set loop variables

(2) compute stiffness matrices  for unloaded configurations

(a) compute Jacobian and Hessian matrices

(b) compute stiffness matrix

(3) main loop

       while  do

(a) recompute end-effector location corresponding loading  (using linearized model)

 

(b) compute equilibrium configurations  and loading  for end-effector loacation ,

apply Algorithm A1                      input:                      output: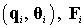

(c) compute residual and loop variable

(d) verify termination condition

(I) if    then    

(II) if              then    

       end (3)

(4) compute end-effector deflection

(5) compute stiffness matrix for parallel manipulator

Previous page  |  Outline  |  Next page