Ecole des Mines de Nantes, 4 rue Alfred-Kastler, Nantes 44307, France
Institut de Recherches en Communications et en Cybernetique de Nantes, 1 rue de la Noe, 44321 Nantes, France
(Submmited to "IEEE Transactions on Robotics", 2011)
Previous page | Outline | Next page
Let us consider now a parallel manipulator, which may be presented as a strictly parallel system of the actuated serial legs connecting the base and the end-platform (Fig. 2) [45]. Using the methodology described in previous section and applying it to each leg, there can be computed a set of m Cartesian stiffness matrices 
expressed with respect to the same coordinate system but corresponding to different platform points (here, the superscript '(i)' denotes the kinematic chain number and it differs from the superscript 'i' in Section III which denotes the iteration number, m is the number of serial kinematic chains in the manipulator architecture). If initially the chain stiffness matrices were computed in local coordinate systems, their transformation is performed in standard way [46], as
 |
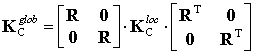(12) |
where 
is a 
rotation matrix describing orientation of the local coordinate system with respect to the global one.
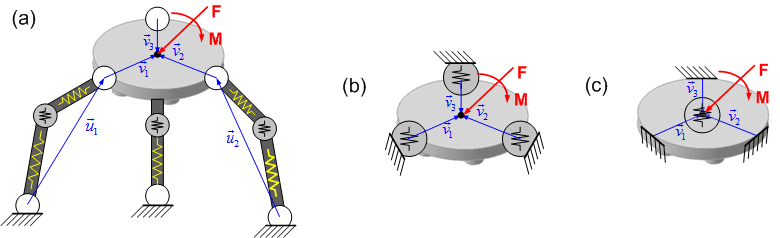
Fig. 2. Typical parallel manipulator (a) and transformation of its VJM models (b, c)
To aggregate these matrices 
, they must be also re-computed with respect to same reference point of the platform. Assuming that the platform is rigid enough (compared to the legs), this conversion can be performed by extending the legs by a virtual rigid link connecting the end-point of the leg and the reference point of the platform (see Fig. 2 where these extensions are defined by the vectors 
).
After such extension, an equivalent stiffness matrix of the leg may be expressed using relevant expression for a usual serial chain, i.e. as 
, where the Jacobian 
defines differential relation between the coordinates of the i-th virtual spring and the reference frame of the end-platform. Hence, using the superposition principle, the final expression for the stiffness matrix of the considered parallel manipulator can be written as
 |
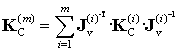(13) |
Besides, it is implicitly assumed here that all stiffness matrices (both for the legs and for the whole manipulator) are expressed in the same global coordinate system. Hence, the axes of all virtual springs are parallel to the axes x, y, z of this system and corresponding Jacobians and their inverses can be easily computed analytically as
 |
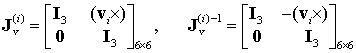(14) |
where 
is a identity matrix of size 
, and
is a skew-symmetric matrix corresponding to the vector 
:
 |
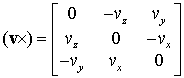(15) |
Therefore, expression allows explicit aggregation of the leg stiffness matrices with respect to any given reference point of the platform. It is worth mentioning that in practice, the matrices 
are always singular while there aggregation usually produce non-singular singular matrix. Relevant examples are presented in Section VI.