Ecole des Mines de Nantes, 4 rue Alfred-Kastler, Nantes 44307, France
Institut de Recherches en Communications et en Cybernetique de Nantes, 1 rue de la Noe, 44321 Nantes, France
(Submmited to "IEEE Transactions on Robotics", 2011)
Previous page | Outline | Next page
In contrast to conventional serial manipulators, whose kinematics does not include passive joints and assures full controllability of the end-effector, parallel manipulators include a number of under-actuated serial chains that are mutually constrained by special connection to the base and to the end-platform. Let us derive an analytical expression for the stiffness matrix of such kinematic chain taking into account influence of the passive joints.
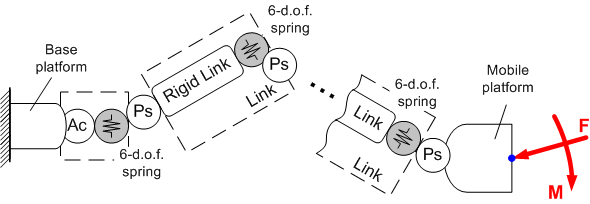
Fig. 1. The VJM model of a general serial chain (Ps – passive joint, Ac – actuated joint)
The kinematic chain under study (Fig.1) consists of a fixed base, a series of flexible links, a moving platform, and a number of actuated or passive joints separating these elements. Following the methodology proposed in our previous publications [30], a relevant VJM model may be presented as a sequence of rigid links separated by passive joints and six-dimensional virtual springs describing elasticity of the links and actuators. For this VJM representation, the direct kinematics is defined by a product of homogeneous transformations that after extraction of end-platform position and orientation is transformed into the vector function
 |
(5) |
where the vector 
includes the position 
and orientation 
of the platform in Cartesian space (Euler angles), the vector 
contains passive joint coordinates, the vector 
collects coordinates of all virtual springs; 
and 
are the sizes of 
and 
respectively.
It can be proven [30] that the static equilibrium equations of this mechanical system may be written as
 |
(6) |
where 
are kinematic Jacobians with respect to the passive and virtual joint coordinates respectively, 
is the external loading (force and torque), and 
the aggregated stiffness matrix of the virtual springs. Using these equations simultaneously with and applying the first-order linear approximation under assumption that corresponding values of the external force 
and the coordinate variations 
are small enough, one can derive the matrix expression
5
 |
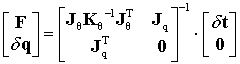(7) |
that allows obtaining the desired Cartesian stiffness matrix 
numerically [30]. Corresponding procedure includes inversion of 
matrix in the right-hand side of and extracting from it the upper-left sub-matrix of the size 
that defines a liner force-deflection relation in Cartesian space:
 |
(8) |
In spite of computational simplicity, the above procedure is not convenient for the parametric stiffness analysis that usually relies on analytical expressions. To derive such expression for the matrix 
, let us apply the blockwise inversion based on the Frobenius formula [42]
 |
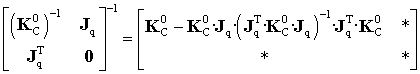(9) |
where 
, that allows to present the desired stiffness matrix as (see Appendix B for details, Eq. B.6)
 |
(10) |
where the first term 
is the stiffness matrix of the corresponding serial chain without passive joints and the second term defines the stiffness decrease due to the passive joints. It worth mentioning that this result is in good agreement with other relevant works [14][43][44] where 
was presented as the difference of two similar components but the second one was computed in a different way.
Analyzing the latter expression (see Appendix A : Properties of stiffness matrix 
), one can get to the following conclusion concerning computational singularities:
Remark 1. The first term of the expression is non-singular if and only if 
, i.e. if the VJM model of the chain includes at least 6 independent virtual springs.
Remark 2. The second term of the expression is non-singular if and only if 
, i.e. if the VJM model of the chain does not include redundant passive joints (i.e. all passive joints are kinematically independent).
Remark 3. If both terms of are non-singular, their difference produces a symmetrical stiffness matrix, which always singular and 
.
Remark 4. If the matrix 
of the chain without passive joints is symmetrical and positive-definite, the stiffness matrix of the chain with passive joints 
is also symmetrical but positive-semidefinite.
Hence, in practice, expression (10) does not cause any computational difficulties and always produce a singular stiffness matrix of rank 
. In analytical computations, it can be also useful the following proposition (see Appendix B: Recursive computation of the stiffness matrix 
) that allows sequential modification of the original stiffness matrix 
in accordance with the following proposition:
Proposition. If the chain does not include redundant passive joints, expression (10) allows recursive presentation
 |
(11) |
where 
and the sub-Jacobians 
are extracted from 
in arbitrary order (column-by-column, or by groups of columns), the superscripts 'i' and 'i+1' define the iteration number.
Corollary. The desired stiffness matrix 
can be computed in 
steps, by sequential application of expression (11) for each column of the Jacobian 
(i.e. for each passive joint separately). If for the i-th iteration, the second term in expression (11) is singular, this step should be skipped (this case corresponds to the so-called redundant passive joint whose influence on the stiffness matrix has been already taken into account at the previous steps)
These results give convenient analytical and numerical computational techniques that are presented in details in Section V.