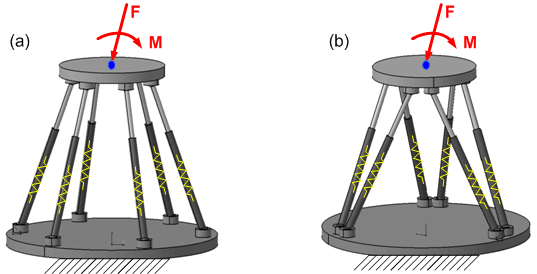
Fig. 3 Geometry of the Stewart-Gough platforms under study
Ecole des Mines de Nantes, 4 rue Alfred-Kastler, Nantes 44307, France
Institut de Recherches en Communications et en Cybernetique de Nantes, 1 rue de la Noe, 44321 Nantes, France
(Submmited to "IEEE Transactions on Robotics", 2011)
Previous page | Outline | Next page
Let apply now the developed technique to computing of the stiffness matrix for two versions of a general Stewart-Gough platform presented in Fig. 3 [43][47][48][49]. It is assumed that in both cases the manipulator base and the moving plate (platform) are connected by six similar extensible legs (Fig. 4) but their spatial arrangements are different:
Fig. 3 Geometry of the Stewart-Gough platforms under study
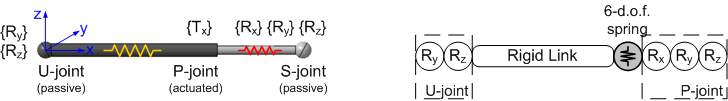
Fig. 4. Geometry of the manipulator leg and its VJM model
Case A: the legs are regularly connected to the base and platform, with the same angular distance 60° (it is obviously degenerate design, where the stiffness matrix should be singular)
Case B: the legs are connected to the base and platform in three pairs, with the angular distance of 120° between the mounting points (it is classical design of Stewart-Gough where the stiffness matrix should be non-singular).
For both designs, the original leg stiffness (i.e. without the passive joints) can be described by the sparse matrix corresponding to the symmetric beam. Further, to take into account influence the passive joints, it should be recursively applied the procedure with the elementary Jacobians
 |
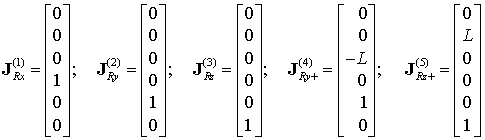(27) |
where L is the leg length. It is obvious that, due to trivial structure of 
, the recursive computations can be easily performed analytically (see subsection V.B.). They sequentially produce the following results:
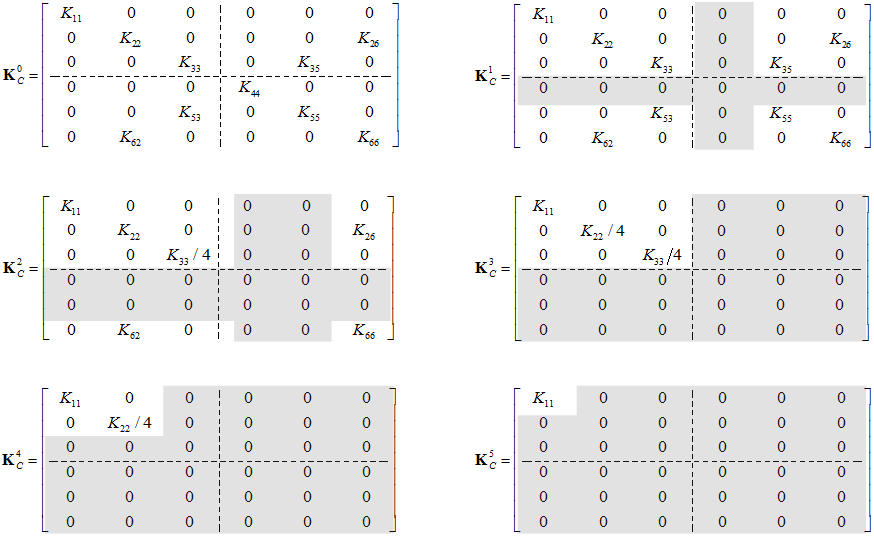
Hence, in final form, the derived matrix includes only the traction/compression term (and not bending, torsion, etc.) what perfectly agrees with other results on Stewart-Gough platforms.
Further, to be applied to each leg, the obtained matrix must be transformed from the local to the global coordinate system. In this specific case, due to the special structure of 
, relevant transformation [24][46]
 |
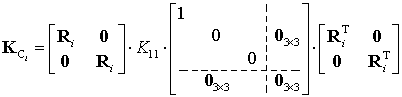(28) |
expressed via the orthogonal rotation matrix 
describing orientation of the i-th local coordinate system with respect to the global one, is easily reduced to
 |
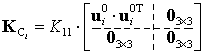(29) |
where 
is the unit vector directed along the leg axis 
(see Fig.2). Besides, before aggregation, the stiffness matrices of separate legs 
must be re-computed with respect to same reference point in accordance with expressions , which yields
 |
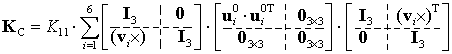(30) |
where 
is the vector from the leg end-point to the platform reference point (see Fig.2). So, after relevant transformations, one can get the final expression of the manipulator stiffness matrix
 |
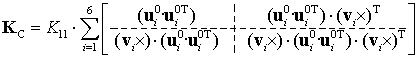(31) |
or
 |
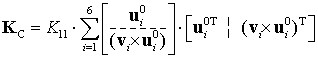(32) |
where the vector 
, 
describing spatial locations of the legs and computed via the direct kinematics, and 
denotes the vector product (in contrast to the above notation 
which is referred to the corresponding skew-symmetric matrix).
The derived equation was applied to both case studies, assuming that the manipulators are in their “home” configurations when the platform is parallel to the base and it is symmetrical with respect to the vertical axis. Corresponding expressions for the leg vectors are
 |
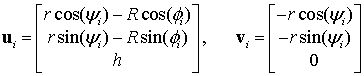(33) |
where 
and 
denote the circle radius which comprise the leg connection point at the base and moving platform respectively,
for the case A, and 
; 
for the case B. Substitution of these vectors to the expression leads to the following stiffness matrices
 |
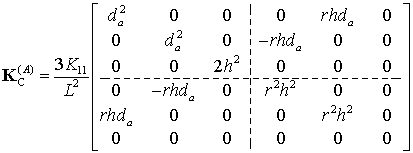(34) |
and
 |
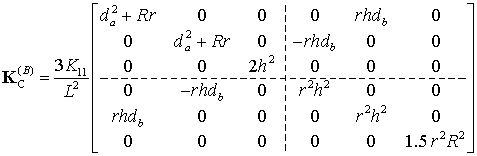(35) |
where 
; 
; 
is the leg length, 
is the vertical distance between the base and the platform, and the superscripts ‘A’ and ‘B’ define the relevant case study. As follows from these expressions, in ‘zero’ location the matrix 
is singular and allows “free” rotation of the end-platform around the vertical axis. In contrast, for the same location the matrix 
is non-singular and the manipulator resists to all external forces/torques applied to the platform. These results are in good agreement with previous research on the Stewart-Gough platforms and confirm efficiency of the developed computational technique for manipulator stiffness modeling [9][47].