from corresponding matrix of the chain without passive joints 
. Assuming that 
, this matrix can be factorised into the product of two non-singular square matrices 
. This yields a compact presentation of the desired matrix in the form Ecole des Mines de Nantes, 4 rue Alfred-Kastler, Nantes 44307, France
Institut de Recherches en Communications et en Cybernetique de Nantes, 1 rue de la Noe, 44321 Nantes, France
(Submmited to "IEEE Transactions on Robotics", 2011)
Previous page | Outline | Next page
Let us analyze in details expression that allows computing the stiffness matrix of a serial chain with passive joints from corresponding matrix of the chain without passive joints . Assuming that , this matrix can be factorised into the product of two non-singular square matrices . This yields a compact presentation of the desired matrix in the form
 |
(A1) |
where
 |
(A2) |
and the inverse 
exists due to the assumption 
. Further, the product 
can be also factorised using the SVD-technique [50] as
 |
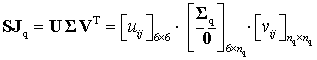(A3) |
where 
, 
are the orthogonal matrices and the matrix 
is composed of 
non-zero singular values 
(provided that 
). The latter gives the following presentation of 
 |
(A4) |
where the product 
may be computed in a straightforward way:
 |
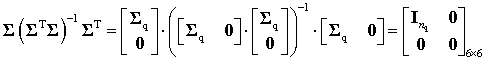(A5) |
So, the inner part of 
may be presented as
 |
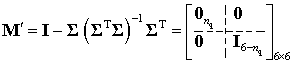(A6) |
This leads to the final expression
 |
(A7) |
that allows to evaluate the rank of the stiffness matrix 
 |
(A8) |
and to justify Remarks presented in Section III.
For computational convenience, the orthogonal matrix 
may be split into six vector columns 
and the matrix product 
is expressed as a subsume of 
corresponding to the non-zero elements of 
. This gives another presentation of the desired Cartesian stiffness matrix
 |
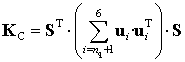(A9) |
where the middle term includes only those unit vectors 
that are not “compensated” by the passive joints (for this notation, the directions 
correspond to the end-effector motion due to the passive joints, which do not produce elastostatic reactions). It should be noted that in the case of 
, i.e. without passive joints, the total sum of 
produces a unit matrix 
and the latter expression is reduced to 
.